I really enjoyed this
Arnold Kling comment on a recent
MR post:
Suppose that the credibility of a scientist is a function of two variables: (1) the evidence he offers; and (2) the strength of his beliefs. I am willing to allow the partial derivative of (2) to be positive and to stipulate Tyler's argument that faking data is a signal of strength of beliefs. But the partial derivative of (1) is much stronger, and fake data enters with a negative sign.
In other words, C=f(E,B), with the first partial derivatives being positive. But, I think the real interest being expressed here is in the nature of the second derivatives, especially the cross partials:
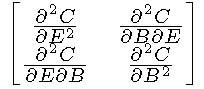
Fundamentally, what are the signs of the off-diagonal elements? As a general rule the Hessian Matrix is symmetric, but would that makes sense in this particular case? The signs on the diagonal elements are interesting too...are there increasing, diminishing, or constant returns to credibility in either evidence or beliefs?
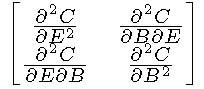 Fundamentally, what are the signs of the off-diagonal elements? As a general rule the Hessian Matrix is symmetric, but would that makes sense in this particular case? The signs on the diagonal elements are interesting too...are there increasing, diminishing, or constant returns to credibility in either evidence or beliefs?
Fundamentally, what are the signs of the off-diagonal elements? As a general rule the Hessian Matrix is symmetric, but would that makes sense in this particular case? The signs on the diagonal elements are interesting too...are there increasing, diminishing, or constant returns to credibility in either evidence or beliefs?
No comments:
Post a Comment